SSAO (Screen space ambient occlusion) is a common post processing effect that approximate how much light is occluded in a given surface by the surrounding objects. In this year SIGGRAPH, there are a few slides in "The Technology behind the Unreal Engine 4 Elemental Demo" about how they implement SSAO. Their technique can either use only the depth buffer or with the addition of per-pixel normal. And I tried to implement both version with a slight modification:
Using only the depth buffer
The definition of ambient occlusion is to calculate the visibility integral over the hemisphere of a given surface:
To approximate this in screen space, we design our sampling pattern as paired samples:
 |
| paired sample pattern |
The AO term for each given pair of samples will be min( (θleft + θright)/π, 1). Then by averaging the AO terms of all the sample pairs (in my case, there are 6 pairs), we achieve the following result:
Dealing with large depth differences
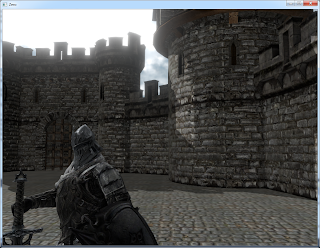
As seen from the above screen shot, there is dark halos around the knight. But the knight should not contribute AO to the castle as he is too far away. So to deal with the large depth differences. I adopt the approach used in Toy Story 3. If one of the paired sample is too far away from the shading point, say the red point in the following figure, it will be replace by the pink point, which is on the same plane as the other valid paired sample:
So we can interpolate between the red point and the pink point for dealing with the large depth difference. Now the dark halo has gone:
The above treatment only handle if one of the paired sample is far away from shading point. What if both of the samples have large depth differences?
|
|
In this case, it will result in the dark halo around the sword in the above screen shot. Remember we are averaging the all the paired samples to compute the final AO value. So to deal with this artifact, we just assign a weight to each paired samples and then re-normalize the final result. Say, for each paired sample, if both of the samples are within a small depth differences, that sample pair will have a weight of 1. If only 1 sample is far away, that pair will have a weight of 0.5. And finally if both of the samples is far away, the weight will be 0. This can eliminate most(but not all) of the artifacts:
Approximating arc-cos function
In this approach, the AO is calculated by using the angle between the paired samples, which need to evaluate the arc-cos function which is a bit expensive. We can approximate acos(x) with a linear function: π(1-x)/2.
And the resulting AO looks much darker with this approximation:
|
|
Note that the maximum error between the two function is around 18.946 degree.
This may affect the AO for the area of a curved surface with low tessellation. You may either need to increase the bias angle threshold or switch to a more accurate function. So my second attempt is to approximate it with a quadratic function: π(1- sign(x) * x * x)/2.
And this approximation shows a much similar result to the one using the arc-cos function.
|
|
And the maximum error of this function is around 9.473 degree.
Using per-pixel normal
We can enhance the details of AO by making use of the per-pixel normal. The per-pixel normal is used for further restricting the angle to compute the AO where the angle θleft, θright are clamped to the tangent plane :
And here is the final result:
Conclusion
The result of this AO is pleasant by taking total 12 samples per pixel and with 16 rotation in 4x4 pixel block at half resolution. I did not apply bilateral blur to the AO result, but applying the blur may gives a softer AO look. Also approximating the arc-cos function with a linear function although is not accurate, but it gives a good enough result for me. Finally more time are need to spend on generating the sampling pattern in the future where the pattern I currently used is nearly uniform distributed (with some jittering).
References
[1] The Technology behind the Unreal Engine 4 Elemental Demo http://advances.realtimerendering.com/s2012/Epic/The%20Technology%20Behind%20the%20Elemental%20Demo%2016x9.pptx
[2] Rendering techniques in Toy Story 3
http://advances.realtimerendering.com/s2010/Ownby,Hall%20and%20Hall%20-%20Toystory3%20(SIGGRAPH%202010%20Advanced%20RealTime%20Rendering%20Course).pdf
[3] Image-Space Horizon-Based Ambient Occlusion
http://www.nvidia.com/object/siggraph-2008-HBAO.html
[4] http://www.wolframalpha.com/
[5] The models are export from UDK and extracted from Infinity Blade using umodel.exe