Photon Mapping Part 2

Introduction
Continue with previous post, this post will describe how light map is calculated from the photon map. My light map stores incoming radiance of indirect lighting on a surface which are projected into Spherical Harmonics(SH) basis. 4 SH coefficients is used  for each color channels. So 3 textures are used for RGB channels (total 12 coefficients).

Baking the light map
To bake the light map, the scene must have a set of unique, non-overlapping texture coordinates(UV) that correspond to a unique world space position so that the incoming radiance at a world position can be represented. This set of UV can be generated inside modeling package or using UVAtlas. In my simple case, this UV is mapped manually.
To generate the light map, given a mesh with unique UV and the light map resolution, we need to rasterize the mesh (using scan-line or half-space rasterization) into the texture space with interpolated world space position across the triangles. So we can associate a world space position to a light map texel. Then for each texel, we can sample the photon map at the corresponding world space position by performing a final gather step just like previous post for offline rendering. So the incoming radiance at that world space position, hence the texel in the light map, can be calculated. Then the data is projected into SH coefficients, stored in 3 16-bits floating point textures. Below is a light map that extracting the dominant light color from SH coefficients:

The baked light map showing the dominant
light color from SH coefficients

Using the light map
After baking the light map, during run-time, the direct lighting is rendering with usual way, a point light is used to approximated the area light in the ray traced version, the difference is more noticeable at the shadow edges.

direct lighting only, real time version

direct lighting only, ray traced version

Then we sample the SH coefficients from the light map to calculate the indirect lighting

indirect lighting only, real time version

indirect lighting only, ray traced version

Combining the direct and indirect lighting, the final result becomes:

direct + indirect lighting, real time version

direct + indirect lighting, ray traced version

As we store the light map in SH, we can apply normal map to the mesh to change the reflected radiance.

Rendered with normal map

Indirect lighting with normal map

We can also applying some tessellation, adding some ambient occlusion(AO) to make the result more interesting:

Rendered with light map, normal map, tessellation and AO

Rendered with light map, normal map, tessellation and AO

Conclusion
This post gives an overview on how to bake light map of indirect lighting data by sampling from the photon map. I use SH to store the incoming radiance, but other data can be stored such as storing the reflected diffuse radiance of the surface, which can reduce texture storage and doesn't require floating point texture. Besides, the SH coefficients can be store per vertex in the static mesh instead of light map. Lastly, by sampling the photon map with final gather rays, light probe for dynamic objects can also be baked using similar methods.

References
March of the Froblins: http://developer.amd.com/samples/demos/pages/froblins.aspx
Lighting and Material of HALO 3: http://www.bungie.net/images/Inside/publications/presentations/lighting_material.zip

Photon Mapping Part 1

Introduction

In this generation of computer graphics, global illumination (GI) is an important technique which calculate indirect lighting within a scene. Photon mapping is one of the GI technique using particle tracing to compute images in offline rendering. Photon mapping is an easy to implement technique, so I choose to learn it and my target is to bake light map storing indirect diffuse lighting information using the photon map. Photon mapping consists of 2 passes: photon map pass and render pass, which will be described below.

Photon Map Pass

In this pass, photons will be casted into the scene from the position of light source. Each photon store packet of energy. When photon hits a surface of the scene, the photon will either be reflected (either diffusely or specularly), transmitted  or absorbed, which is determined by Russian roulette. 

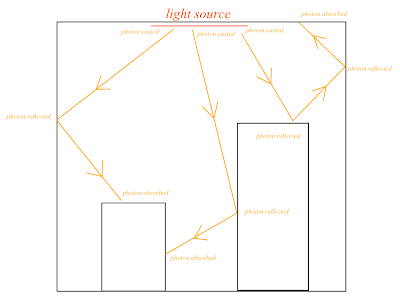Photons are traced in the scene to simulate the light transportation

This hit event represents the incoming energy of that surface and will be stored in a k-d tree (known as photon map) for looking up in the render pass. Each hit event would store the photon energy, the incoming direction and the hit position.

However, it is more convenient to store radiance than storing energy in photon because when using punctual light source(e.g. point light), it is hard to compute the energy emits given the light source radiance. So I use the method described in Physically Based Rendering, a weight of radiance is stored in each photon:

When a photon hits a surface, the probability of being reflected in a new random direction used in Russian roulette is:

This probability equation is chosen because photon will have a higher chance of being reflected if it is brighter. If the photon is reflected, its radiance will be updated to:

And the photon will continue to trace in the newly reflected direction.

Render pass

In render pass, the direct and indirect lighting is computed separately. The direction lighting is computed using ray tracing.

Direct light only

The indirect lighting is computed by sampling from the photon map. When calculating the indirect lighting in a given position(in this case, the shading pixel), we can locate N nearby photons in photon map to estimate the incoming radiance using kernel density estimation. A kernel function need to satisfy the conditions:

I use the Simpson's kernel(also known as Silverman's second order kernel) suggested in the book Physically Based Rendering:

Then the density can be computed using kernel estimator for N samples within a distance d (i.e. the distance of the photon that is the most far away in the N samples):

Then the reflected radiance at the shading position can be computed with:

However, the result showing some circular artifact:

Using the photon map directly for indirect diffuse
light would show artifact

To tackle this problem, either increase the number of photon to a very high number, or we can perform a final gather step. In the final gather step, we shoot a number of final gather rays from the pixel that we are shading in random direction over the hemisphere of the shading point.

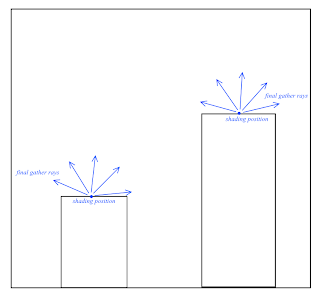Final gather rays are casted from every shading position

When final gather ray hit another surface, then the photon map is queried just like before and the reflected radiance from this surface will be the incoming radiance of the shading pixel. Using Monte Carlo integration, the reflected radiance at the shading pixel can be calculated by sampling the final gather rays. Here is the final result:

Direct light + Indirect light, with final gather

Indirect light only, with final gather

Conclusion

In this post, the steps to implement photon map is briefly described. It is a 2 passes approach with the photon map pass building a photon map as kd-tree representing the indirect lighting data and the render pass use the photon map to compute the final image. In next part, I will describe how to make use of the photon map to bake light map for real time application.

References

A Practical Guide to Global Illumination using Photon Maps: http://nameless.cis.udel.edu/class_data/cg/jensen_photon_mapping_tutorial.pdf
Physically Based Rendering: http://www.pbrt.org/