Studying "Spectral Primary Decomposition"

Introduction

It has been a long time since my blog post (because of Covid, work, Elden Ring...). So I decided to study the "Spectral Primary Decomposition for rendering with sRGB Reflectance", which used in previous posts, to recall my memory. It is an efficient technique to up-sample sRGB texture to spectral reflectance by multiplying the sRGB values with 3 precomputed basis functions:

Overview of "Spectral Primary Decomposition" from the Explanatory Poster

In this post, I would like to find an efficient spectral up-sampling method which also support wider gamut (e.g. Display-P3...) or investigate why this technique does not support wider gamut.

Porting to Octave

In the paper, it provides sample source code written in Matlab. Since I do not have a Matlab license, so the first thing I need to do is to port the source code to the open source Octave (ported source code can be found here). During the porting process, the fmincon() used for finding the 3 spectral primary basis functions in Octave does not work, so I switched to use sqp() instead (also removed the linprog() from original source code).

Basis Functions generated in Octave

The resulting graph is not as smooth as the original paper. So I decided to try different initial value for the objective function. I chose a normalized Color Matching Function:

Basis Functions generated with normalized CMF initial value

Code for generating normalized CMF initial value

The resulting curves look smoother with normalized CMF as initial value. Also, during the porting process, I switched to use CMF2006 2 degree observer instead of CMF1931 / 2006 10 degree observer used in original source code.

Working with wider gamut

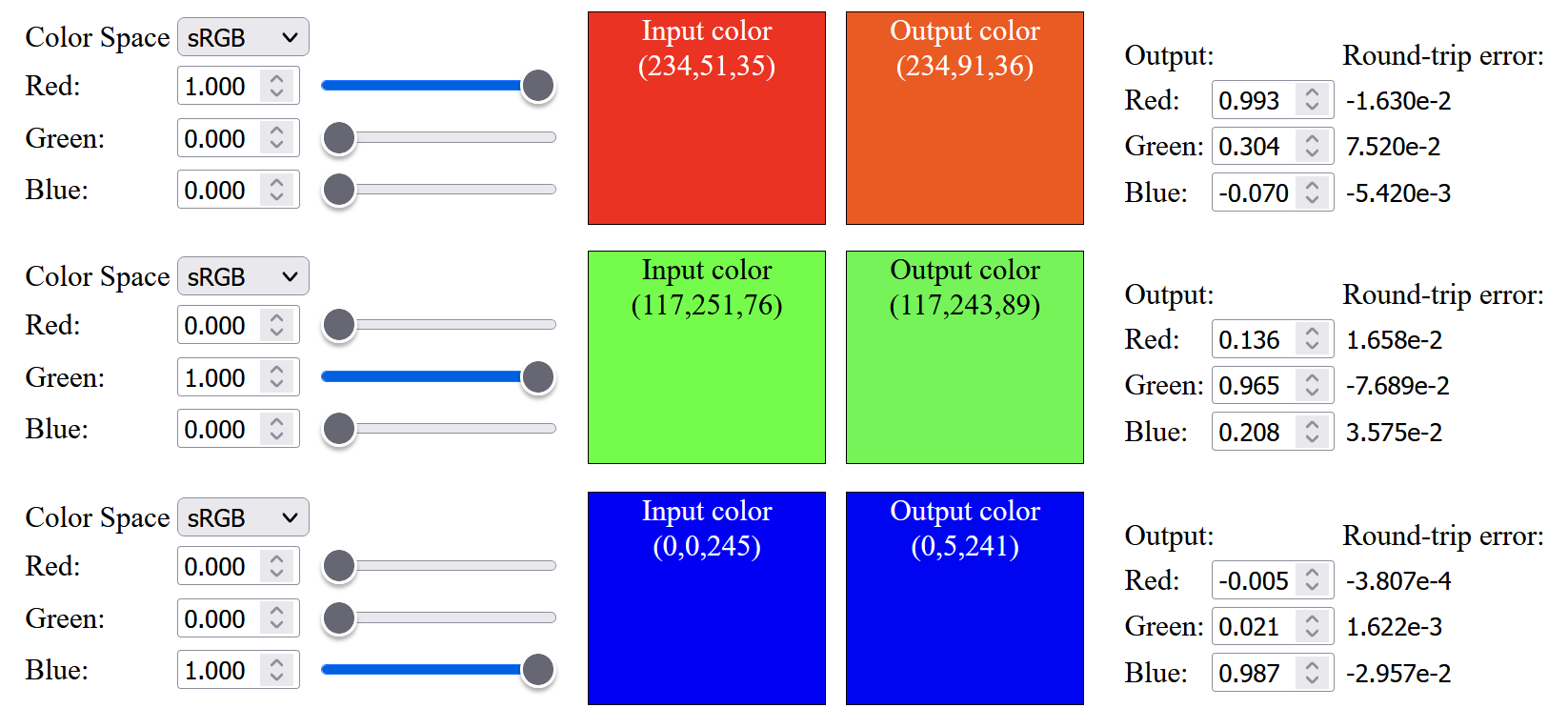
So the next step is to change the color primaries from sRGB to Display-P3 (which the original source listed as infeasible). As expected, the result is not good, not only saturated color cannot be up-sampled, the color within the sRGB gamut are not similar to the original color, and saturated red color will have an orange tint after up-sampling: (Note that below images have Display-P3 color profile attached, to view those saturated color outside sRGB gamut, a wide gamut monitor is needed)

Up-sampled saturated sRGB color

Up-sampled saturated P3 color

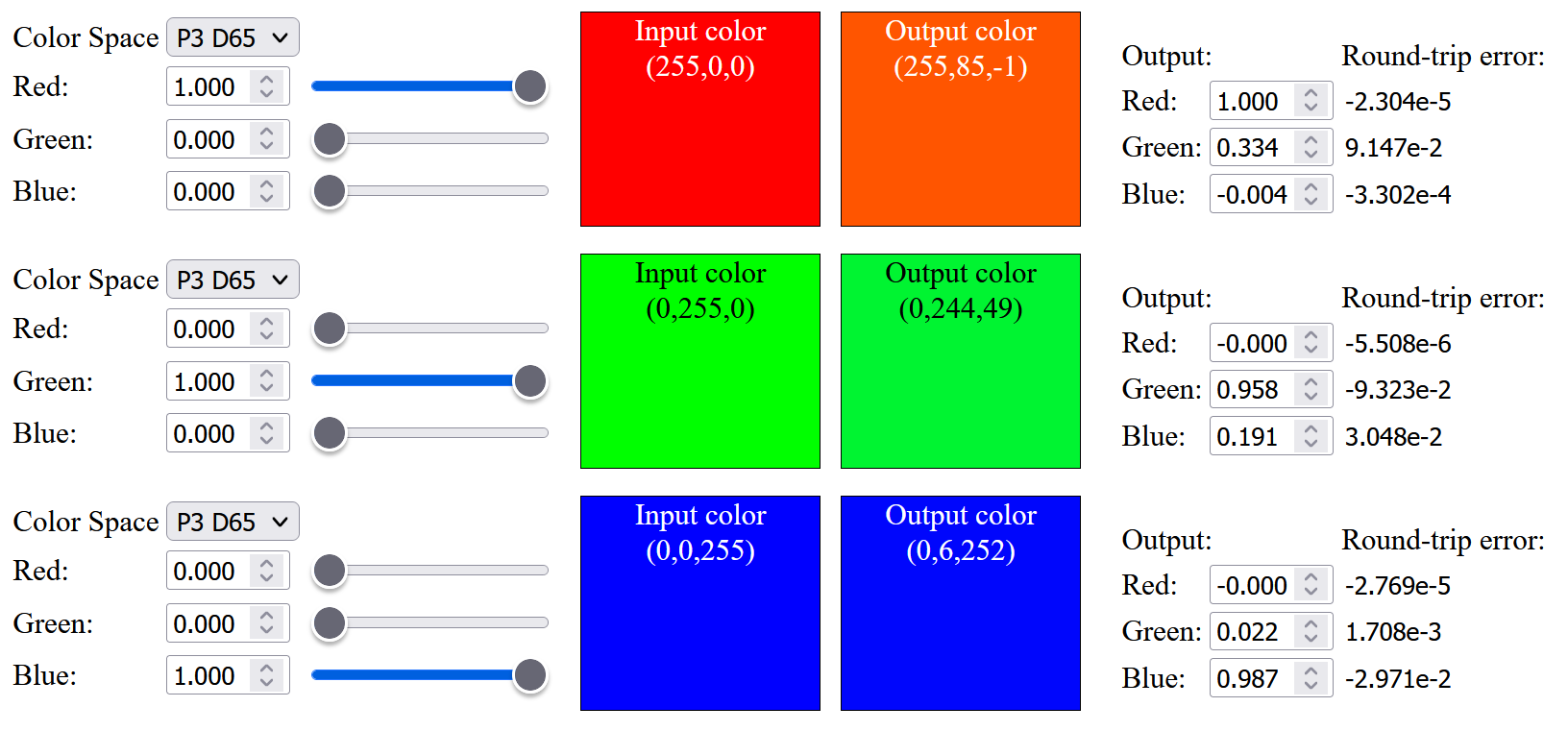
So, I tried to modify the objective function opt_fn() used in sqp() to include a weight to minimize the sRGB primaries color difference:

Code snippet of the objective function with sRGB primaries weight

The result improves a bit and the up-sampled saturated red has a less orange tint:

Up-sampled saturated sRGB color with sRGB primaries weight

Up-sampled saturated P3 color with sRGB primaries weight

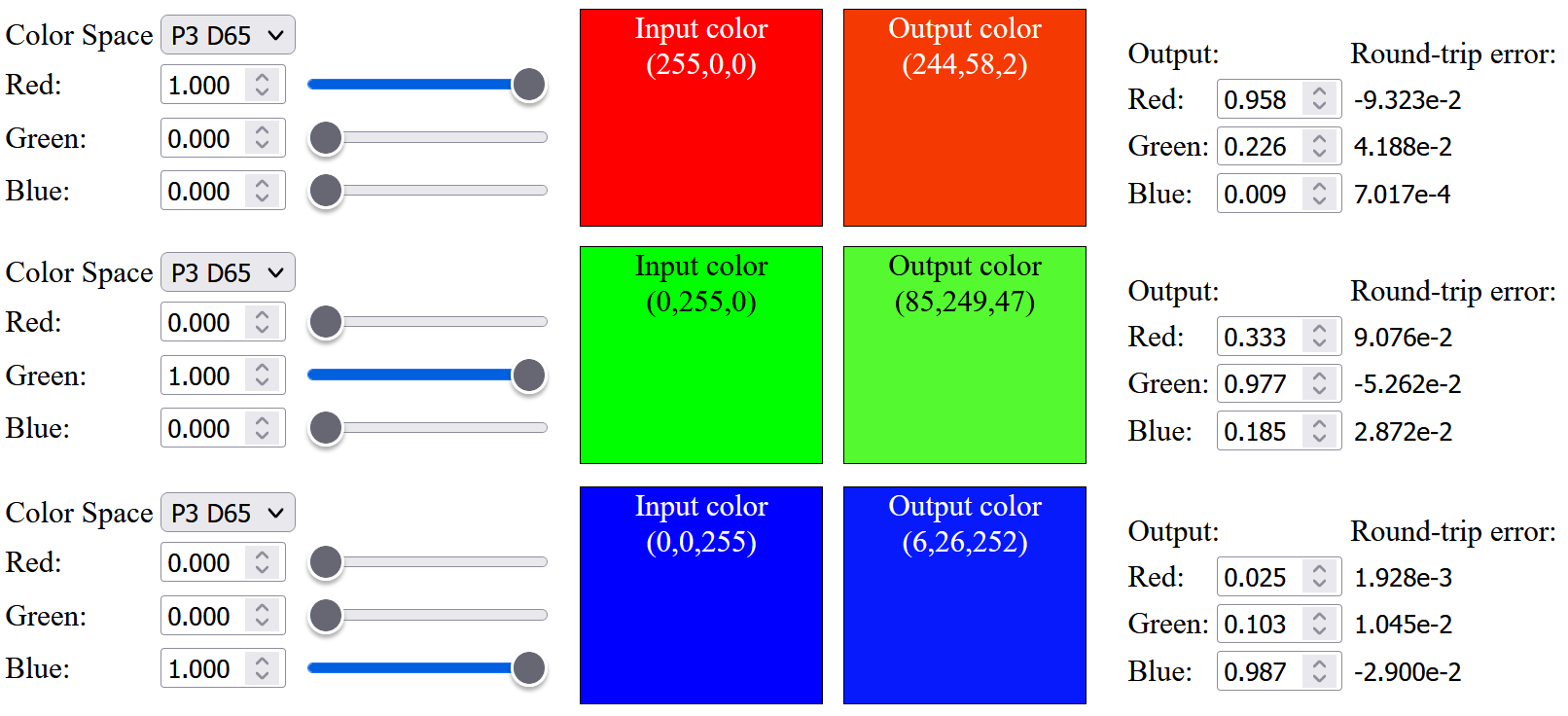
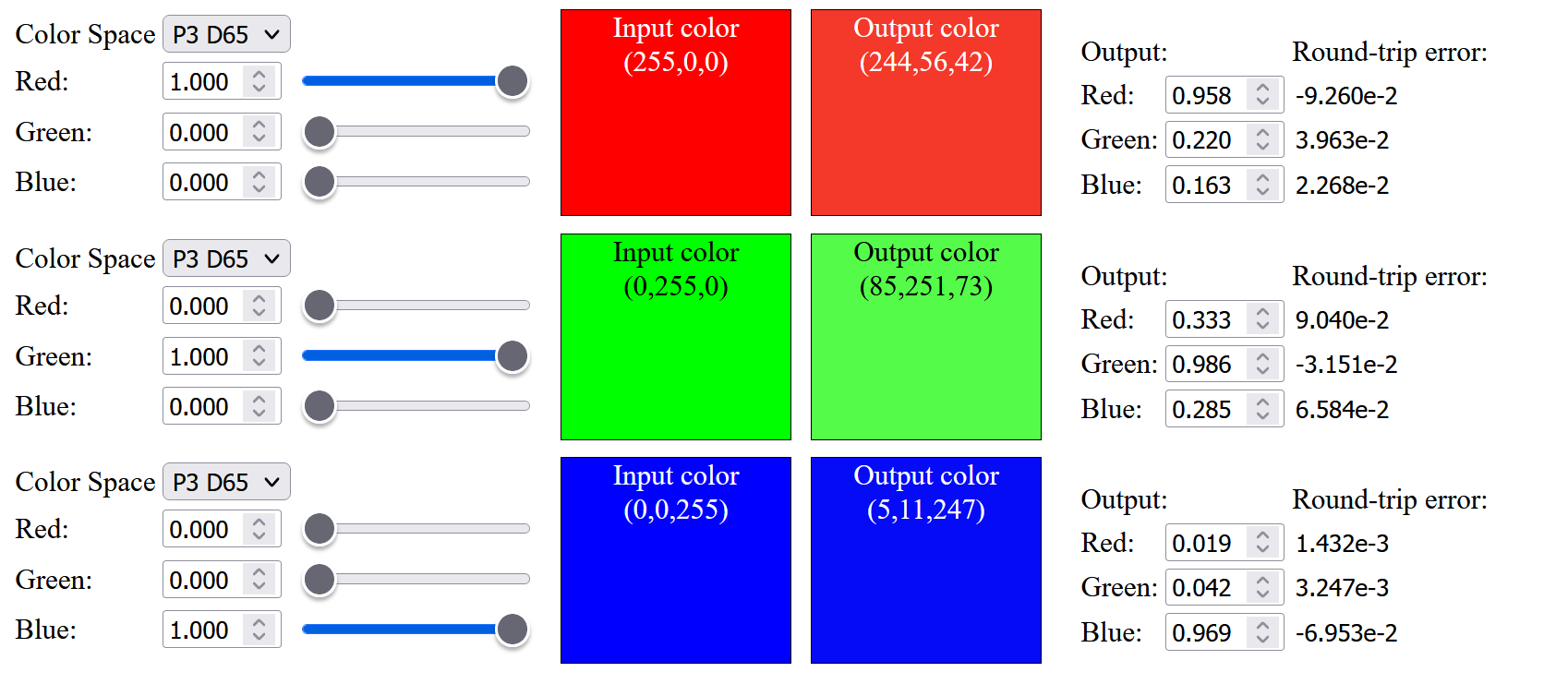
Up to this point, all the precomputed spectral primary basis functions are within [0, 1] range (i.e. to not reflect more light in each basis function), I was wondering what if we relax this constraint and enforce this limit after linearly combining all the basis functions. I have tried to relax the range of individual basis function to [-0.05, 1.05], [-0.075, 1.075] and [-0.1, 1.1] (details can be found in the visualization website from modified source code). With the relaxed range, we can get very similar sRGB color after up-sampling:

However, for those saturated Display-P3 color, we still cannot up sample them exactly, and can only achieve slightly more saturated color compared to sRGB color:

The up-sampled saturated red is having a visible difference from the original color before up-sampling, I have tried to modify the objective function to only optimize the Red basis function (ignoring the Green and Blue basis functions), and still cannot get an exact up-sampled saturated red from a D65 light source. May be it is impossible to produce the most saturated Display-P3 red with a D65 light source without violating the physical constraint.

Out of curiosity, I tried to plot the chromaticity diagram of the up-sampled color. The result shows that, using limited [0, 1] range, the up-sampling process can produce "more color" (but not accurate, e.g. red color will be up-sampled to "orange-red"), while using relaxed constraint will reduce the up-sampled color gamut.

Chromaticity diagram of up-sampled color using limited [0, 1] range

Chromaticity diagram of up-sampled color using relaxed [-0.1, 1.1] range

CMF Reference White

Up to this point, the calculation for the up-sampled color is using D65 as reference white. But one day, I saw this tweet:

The CMF is using an equal-energy white as its reference white. So I was wondering whether all my calculation was wrong and should add chromatic adaptation after CMF integration.

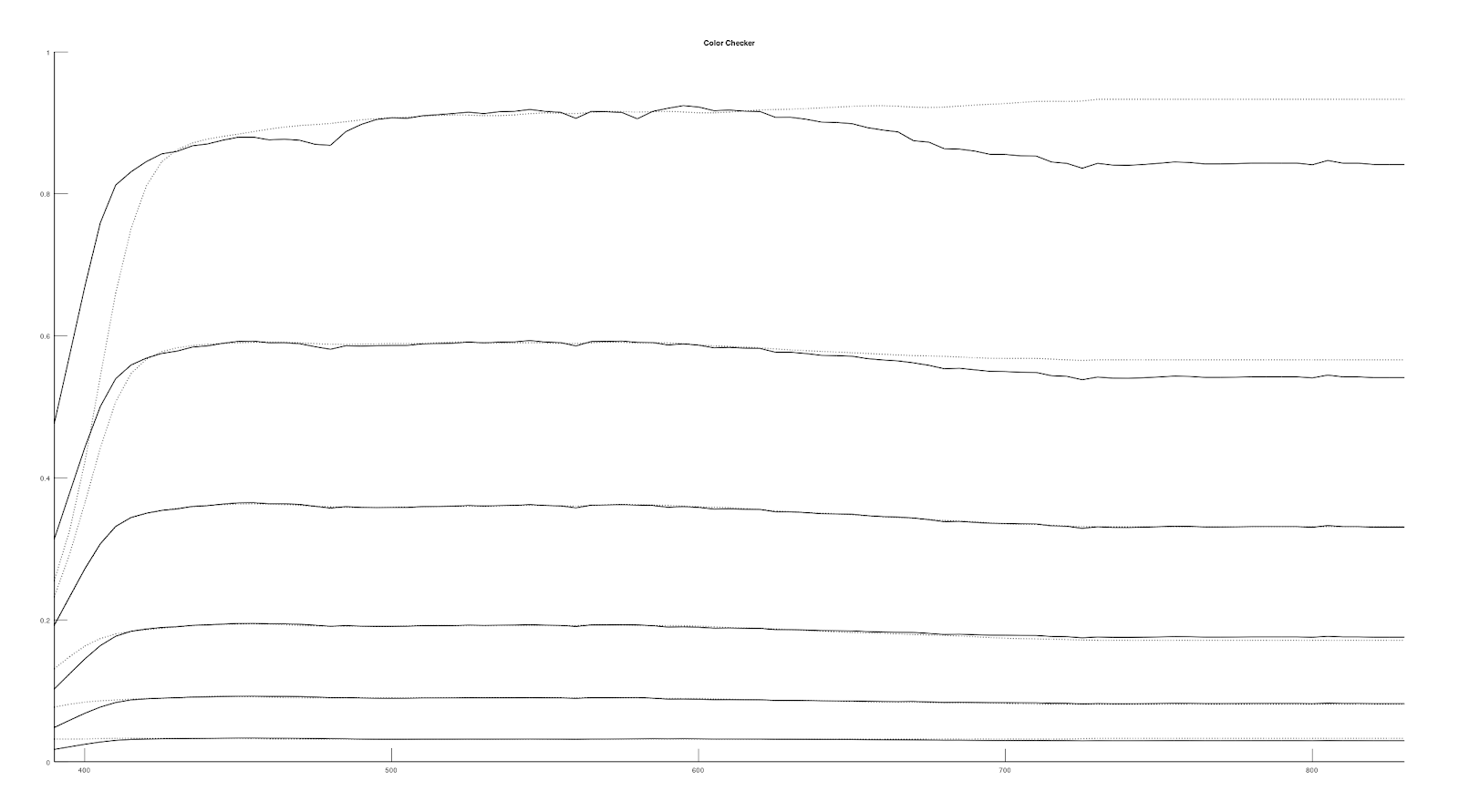
So, I decided to find the spectral reflectance of color checker to integrate with the CMF to verify whether chromatic adaption are needed after CMF integration. Using the color checker data found from here, illuminating those grey patches with D65 and then integrate the result with CMF get the following results:

Illuminating grey patches with D65, integrate with CMF without CAT from Illuminant E

sRGB value of measured Color Checker (2005)

Our computed sRGB value are very similar to the measured data, so it seems like we don't need an extra chromatic adaption to adapt the color from the CMF equal-energy reference white (or please let me know if my maths are incorrect).

Optimizing up sampling function with  Color Checker Data

After working with color checker data, I came up with an idea to modify the spectral basis objective function to include a weight to bias it to match with the neutral 6.5 grey patch spectral reflectance data. We can get a decent match for the up-sampled spectral reflectance of color checker grey patches (i.e. white 9.5, neutral 8, neutral 6.5, neutral 5, neutral 3.5, neutral 2).

Spectral Basis computed for Display-P3	Spectral Basis weighted with Neutral 6.5 color checker patch
Up-sampled spectral reflectance of color checker grey patches using Spectral Basis computed for Display-P3	Up-sampled spectral reflectance of color checker grey patches using Spectral Basis weighted with Neutral 6.5 patch data

However, the up-sampled white color will have a slight round-trip error:

Conclusion

In this post, I have ported the original "Spectral Primary Decomposition" source code to Octave, tried to change it to up-sample Display-P3 color, but the result is not very good. Also, within a game engine, we usually have exposure and tone mapping adjustment, which affect the final pixel color. So I was wondering whether the up-sampling method should take those parameters into account. But doing so, the texture color meaning will be different from the PBR albedo texture. So, I will leave it for future investigation.

References

[1] https://graphics.geometrian.com/research/spectral-primaries.html

[2] http://yuhaozhu.com/blog/cmf.html 

[3] https://babelcolor.com/colorchecker-2.htm

Color Matching Function Comparison

Introduction

When performing spectral rendering, we need to use the Color Matching Function(CMF) to convert the spectral radiance to XYZ values, and then convert to RGB value for display. Different people have a slight variation when perceiving color, and age may also affect how color are perceived too. So the CIE defines several standard observers for an average person. The commonly used CMF are CIE 1931 2° Standard Observer and CIE 1964 10° Standard Observer. Beside these 2 CMF, there also exist other CMF such as Judd and Vos modified CIE 1931 2° CMF and CIE 2006 CMF. In this post, I will try to compare the images rendered with different CMF (as well as some analytical approximation). A demo can be downloaded here (the demo renders using wavelength between [380, 780]nm, which may introduce some error with CMF that have a larger range).

Left: rendered with CIE2006 CMF
Right: rendered with CIE1931 CMF

CMF Luminance

When I was implementing different CMF into my renderer, replacing the CMF directly will result in slightly different brightness of the rendered images:

Rendered with 1931 CMF

Rendered with 1964 CMF

This is because the renderer uses photometric units (e.g. lumen, lux..) to define the brightness of the light sources. Since the definition of luminous energy depends on the luminosity function (usually the y(λ) of CMF), we need to calculate the intensity of the light source with respect to the chosen CMF. Using the correct luminosity function, both rendered images have similar brightness:

Rendered with 1931 CMF

Rendered with 1964 CMF + luminance adjustment

 

CMF White Point

When using different CMF, the white point of different standard illuminant will be slightly different:

White point from wikipedia

Since we are dealing with game texture, color are usually defined in sRGB with a D65 white point, we need to find the white point of the D65 illuminant for the CMF that will be tested in this post. Unfortunately, I can't find D65 white point for the CIE 2006 CMF on the internet, so I calculated it myself (The calculation steps can be found in the Colab source code):

CIE 2006   2° : (0.313453, 0.330802) 

CIE 2006 10° : (0.313786, 0.331275)

But when I rendered some images with and without chromatic adaptation, the result looks similar:

1964 CMF without chromatic adaptation

1964 CMF with chromatic adaptation

So I searched on the internet, I can't find any information whether we need to chromatic adapt the rendered image due to different white point when using different CMF... May be this is because the difference is so small that applying chromatic adaptation makes no visible difference. 

CIE 2006 CMF analytical approximation

The popular CIE 1931 and 1964 CMF have simple analytical approximation, such as: "Simple Analytic Approximations to the CIE XYZ Color Matching Functions" (which will be tested in this post). The newer CIE 2006 CMF lacks such an approximation. So I derived one using similar methods and the curve fitting process can be found in the Colab source code.

2006 2° lobe approximation:

2006 2° lobe approximation shader source code

black lines: exact 2006 2° CMF color lines: approximated 2006 2° CMF

2006 10° lobe approximation:

2006 10° lobe approximation shader source code

black lines: exact 2006 10° CMF color lines: approximated 2006 10° CMF

Saturated lights comparison

With the above changes to the path tracer, we can render some images for comparison. A scene with several saturated lights using sRGB color (1,0,0), (1,1,0), (0,1,0), (0,1,1), (0,0,1), (1,0,1) is tested (which will be spectral up-sampled). 10 different CMF are used:

• CIE 1931 2° 
• CIE 1931 2° with Judd Vos adjustment
• CIE 1931 2° single lobe analytic approximation
• CIE 1931 2° multi lobe analytic approximation
• CIE 1964 10° 
• CIE 1964 10° single lobe analytic approximation
• CIE 2006 2°
• CIE 2006 2° lobe analytic approximation
• CIE 2006 10°
• CIE 2006 10° lobe analytic approximation

Here are the results:

CIE 1931 2°	CIE 1931 2° with Judd Vos adjustment
CIE 1931 2° single lobe analytic approximation	CIE 1931 2° multi lobe analytic approximation
CIE 1964 10°	CIE 1964 10° single lobe analytic approximation
CIE 2006 2°	CIE 2006 2° lobe analytic approximation
CIE 2006 10°	CIE 2006 10° lobe analytic approximation

From Wikipedia:

"The CIE 1931 CMF is known to underestimate the contribution of the shorter blue wavelengths."

So I was expecting some variation for the blue color when using different CMF. But to my surprise, only the CIE 1931 CMF suffer from the “Blue Turns Purple” Problem (Edited: As pointed out by troy_s on twitter, the reference I provided was wrong, the link talks about psychophysical effect, while the current issue is mishandling of light data) which we have encountered in previous posts (i.e. saturated sRGB blue light will render purple color). Originally, after previous blog post, I was investigating this issue and was suspecting the ACES tone mapper cause the color shift (as this issue does not happen when rendering in narrow sRGB gamut with Reinhard tone mapper). I was thinking may be we can use the OKLab color space to get the hue value before tone mapping and tone map only the lightness to keep the blue color. But when I tried with this approach, the hue value obtained before tone mapping is still purple color, which suggest may not be the tone mapper causing the issue (or somehow my method of getting the hue value from HDR value is wrong...). So I have no idea on how to solve the issue and randomly toggle some debug view modes. Accidentally, I found that some of the purple color are actually inside my AdobeRGB monitor display gamut (but outside the sRGB gamut on another monitor...), so the problem is not only caused by out of gamut color producing the purple shift...

The purple color on the wall is within displayable Adobe RGB gamut

Highlighting out of gamut pixel with cyan color

So I decided to investigate the problem for spectral renderer first (and ignore the RGB renderer), and that's why I tested different CMF in this blog post. (Also, as a side note, the behavior for the blue turns purple color problem is a bit different between RGB and spectral renderer, using a more saturated blue color, e.g. (0, 0, 1) in Rec2020, can hide this issue in RGB renderer while using the same more saturated blue color with 1931 CMF spectral renderer still suffer from the problem, while other CMF doesn't have this issue.)

 

Color Checker comparison

Next, we compare a color checker lit by a white light source. Since my spectral renderer need to maintain compatibility with RGB rendering and I was too lazy to implement spectral material using measured spectral reflectance, so both the color checker and the light source are up-sampled from sRGB color.

CIE 1931 2°	CIE 1931 2° with Judd Vos adjustment
CIE 1931 2° single lobe analytic approximation	CIE 1931 2° multi lobe analytic approximation
CIE 1964 10°	CIE 1964 10° single lobe analytic approximation
CIE 2006 2°	CIE 2006 2° lobe analytic approximation
CIE 2006 10°	CIE 2006 10° lobe analytic approximation

From the above results, different CMF have similar looks except the blue color.

Conclusion

In this post, we have compare different CMF, provided an analytical approximation for the CIE 2006 CMF and calculate the D65 white point for CIE 2006 CMF (the math can be found in the Colab source code). All the CMF produce similar color except the blue color, with CMF newer than the 1931 CMF can render saturated blue color correctly without turning it into purple color. May be we should use newer CMF instead, especially when working with wide gamut color. And the company Konica Minolta points out that: the CIE 1931 CMF has issue with wider color gamut with OLED display (which suggest to use CIE 2015 CMF instead). But sadly, I cannot find the data for CIE 2015 CMF, so it is not tested in this post.

Reference

[1] https://en.wikipedia.org/wiki/CIE_1931_color_space

[2] http://cvrl.ioo.ucl.ac.uk/

[2] http://jcgt.org/published/0002/02/01/paper.pdf

[3] https://en.wikipedia.org/wiki/ColorChecker

[4] https://en.wikipedia.org/wiki/Standard_illuminant

[5] https://www.rit.edu/cos/colorscience/rc_useful_data.php

[6] https://sensing.konicaminolta.asia/deficiencies-of-the-cie-1931-color-matching-functions/